一题多解八数码难题

一题多解八数码难题

    详细C++代码见我校左俊伟同学博客：http://zjwer.umi.pw/?p=198

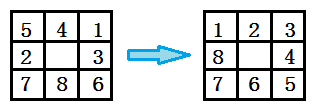
八数码问题是一个比较经典的路径搜索问题。八数码是一个九宫格，其中有八个格子有数字，还有一个格子是空位，和空位相邻的数字格子可以和空位相互交换，游戏的最终目的就是让这些数字形成一个有序的局面。假如说我们有左边这样一个初始状态，我们现在就是想找到一种最快捷的方法，使左边的初始状态转换为右边的最终状态。

       对于求对小的移动次数，我们可以想到一种常用的方法宽搜。

如果按照BFS的思路，我们每次扩展四个节点，分别是空格上移、下移、左移和右移（当然，大多数节点是无法完全扩展这四个方向的），一层层搜索之后，直到发现了目标状态，由此就可以得到一个步数最少的解法了。

这道题用宽搜会有重复的搜索，如何判重就是使用宽搜的难点了。

康托展开+单向宽搜

康拓展开是一个很好的解决判重的工具。

我们可以发现对于每个格子上的数字在棋盘上都是唯一的（只出现一次），而且0-9每个数字都一定会出现。如果把每个数字排成一列的话，形成的序列可以看做0-9这9个数字的全排列中的一个序列。

我们把序列 0 1 2 3 4 5 6 7 8 9 作为全排列的第一小， 0 1 2 3 4 5 6 7 9 8 作为全排列的第二小，以此类推。

这样我们就可以确信对于每一个序列都有唯一一个数字与之相匹配。这就是一个很好的判重工具。

那么我们怎样快速的计算这个数值呢？康拓展开就可以很好的解决这个问题。如果我们想知道321是{1,2,3}的全排列中第几小的数。

     可以这样考虑：第一位是3，小于3的数有1、2 。所以有2*2!个。