信息学奥赛之窗--进制

一、进制相关知识
1.进制表示

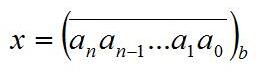
   表示b进制下的n+1位数。  
2.进制之间的转换

• b进制向十进制转换（按权值展开）
   
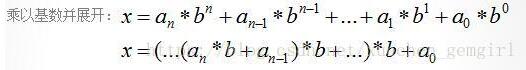
  十进制向b进制转换：
  

• 整数部分除以基数并倒取余数。

• 小数部分乘以基数，并顺取整数部分

二、题目
1.【天平I】
一个天平，有N个重量未知的砝码，砝码重量可由你自由确定。砝码可任意放在天平的左右两边，但要求称出从1到M之间所有的重量，现给出N的值，请问M最大值为多少。
【分析】如下图分析

2.【天平II】
一个天平，砝码分别为1g、3g、9g、27g、…、6561g…，每个砝码只有一个，要称重的物品放在天平的左侧，而砝码允许放在天平的左右两侧。已知一个物品的质量N （N≤10^8 ），问如何称重？
【分析】
　　因为砝码可以放右侧、不放或者放左侧三种状态，因此可以将N转换成三进制后，将三进制中的0、1、2三个状态转换成 0、1 、-1 ，具体的说，就是0和1不变，2变成-1后，其高一位加1。

3.【天平III】
一个天平，砝码分别为1g、3g、9g、27g、… 、6561g…，每个砝码只有一个，要称重的物品放在天平的左侧，而砝码只允许放在天平的右侧。将由这个系统可以称出来的重量按从小到大的顺序进行排列，得到下列序列：1,3,4,9,10,…。问其中的第K个重量是多少？(数据规模：K≤10^5)
【分析】
　　只允许放右侧，那么对于一个砝码只有两种状态，要么放，要么不放，那么可以用二进制来处理。将K转化为二进制，从低到高对应位上是1，则对应从小到大的对应砝码就使用，是0则表示该砝码未用。

4.有一个黑匣子，黑匣子里有一个关于 x 的多项式 p(x) 。我们不知道它有多少项，但已知所有的系数都是正整数。每一次，你可以给黑匣子输入一个整数，黑匣子将返回把这个整数代入多项式后的值。你可以在几步之内还原出整个多项式？
【分析】
      首先,输入 1 ,于是便得到整个多项式的所有系数之和.不妨把这个系数和记作 S .下一步,输入 S + 1 ,于是黑匣子返回
     an * (S + 1)＾n + an-1 * (S + 1)＾n-1 + … + a1 * (S + 1)＾１ + a0
把这个值转换成 S + 1 进制,依次计算出每一位上的数,它们就是多项式的各项系数了。
　　为什么是S+1?
－－确保进制的基数大于最大的系数，第二次带入就应为系数和+1。